这部分是double complex的一些内容, 内容比较少, 主要就是为了给后面的kunneth formula有个基本的定义啥的, 不考虑Tot函子的整体性质整块内容也没啥需要证明的, 摸了.👻 Stack Project 里面有很全的内容.
Double Complex
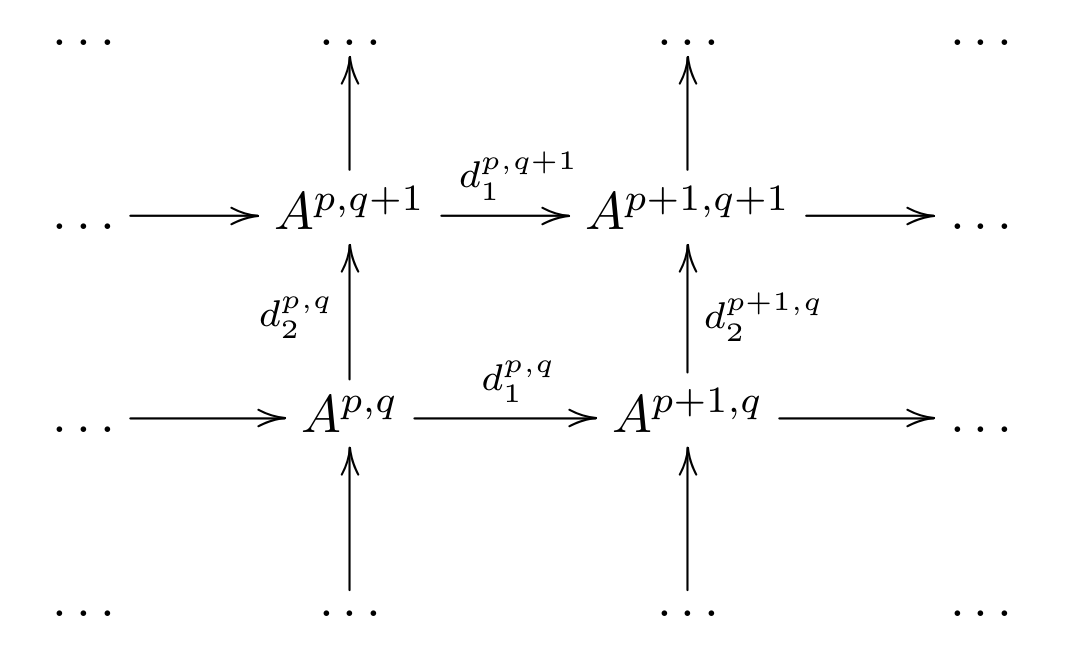
Definition 1. Let A be an addictive category. A double chain complex A is given by {Ap,q,dp,q1,dp,q2}p,q∈Z where dp,q1:Ap,q→Ap−1,q and dp,q2:Ap,q→Ap,q−1 are morphisms of A s.t. the following conditions hold:
1. dp−1,q1∘dp,q1=0;
2. dp,q−12∘dp,q2=0;
3. dp,q−11∘dp,q2=dp−1,q2∘dp,q1.
for all p,q∈Z.
The definition of double cochain complex is similar.
Definition 2. For a double complex, its total complex Tot(C) is given by Tot(C)n=⊕p+q=nCp,q with the differential morphism dnTot=∑p+q=n(dp,q1+dp,q2). We can verify dnTot∘dn+1Tot=0.
Notice that in abelian category we may not have ⊕p+q=nCp,q. Then we can use ∏p+q=nCp,q to substitute it. We can define the homology on the partial chain complex (Ap,q,dp,q1) and
(Ap,q,dp,q2).
Definition 3. For two complex C,D, we can define the tensor product of C and D as TotB, where Bp,q=Cp⊗Dq, dp,q1=dp,q⊗id, dp,q2=(−1)pid⊗dp,q, dnTot=∑p+q=ndp,q1+dp,q2.
Definition 4. For two complex C,D, we can define the Hom of C and D as TotB, where Bp,q=Hom(C−p,Dq), dp,q1(f)(c)=(−1)p+q+1fdp−1(c), dp,q2(f)(c)=dpf(c).
Proposition 1. Morphisms f:C→C′, g:D→D′ induce chain complex maps
f⊗f:C⊗D→C′⊗D′
Hom(f,g):Hom(C′,D)→Hom(C,D′)
If f≃f′ and g≃g′, then f⊗g≃f′⊗g′, Hom(f,g)≃Hom(f′,g′).
Proposition 2. If C≃C′, D≃D′, then C⊗D≃C′⊗D′, Hom(C,D)≃Hom(C′,D′).